При каких значениях с прямая y=c имеет с графиком три общие точки

Постройте график функции  y = x²— 3|x| — x  и определите, при каких значениях    c прямая   y = c имеет с графиком три общие точки.

Вспомним модуль числа.

|x| = x, если x неотрицательное число (больше нуля или равно нулю)

|x| = — x, если x < 0

Преобразуем функцию.

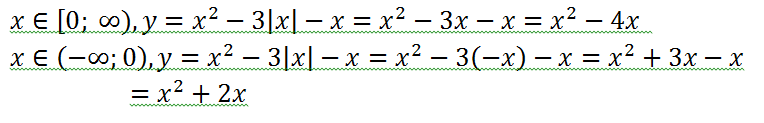
Итак, функция приобрела вид:

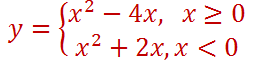
Постройте график функции y = x2- 3|x| — x и определите, при каких значениях   прямая   имеет с графиком три общие точки.

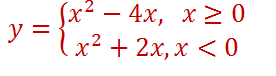
Найдем несколько основных точек для каждой параболы и схематично их изобразим.

Вершина параболы А(m; n)
A(2; — 4)

Точка пересечения параболы с осью ординат:
В(0; с),   В(0; 0)

Точки пересечения параболы с осью абсцисс (нули функции).
x = 0; x = 4

Теперь найдем основные точки для другой функции.

Вершина параболы A(-1; -1)

Точка пересечения параболы с осью ординат:
В(0; с),   В(0; 0)

Точки пересечения параболы с осью абсцисс (нули функции).
x = 0; x = -2

Строим графики.

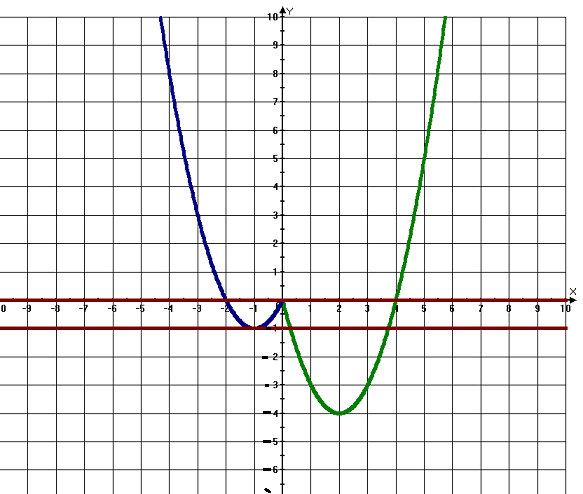
Прямая y = c имеет с графиком функции три общие точки, если

c = 0, c = -1.

Смотрите видеоурок с подробным решением задачи.