Постройте график функции  y = |x -2| -|x + 1) + x — 2

Постройте график функции  y = |x -2| -|x + 1) + x — 2 и найдите значения m , при которых прямая y = m  имеет с ним ровно две общие точки.

Вспомним модуль числа.

|x| = x, если x
|x| = — x, если x < 0

Если под знаком модуля содержится положительное число или ноль, прямые скобки убираем, а выражение переписываем без изменения.

Если под знаком модуля содержится отрицательное число , прямые скобки убираем, а выражение заменяем ему противоположным

Преобразуем функцию. Составим и решим 4 системы неравенств.

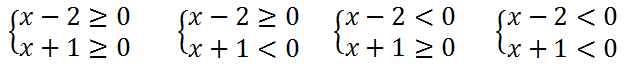
Решаем первую систему:

Аналогично решаем еще три системы, затем записываем окончательный вид функции.

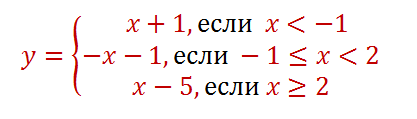
Каждая часть функции является линейной функцией. Для построения графика достаточно взять для каждой части две точки на заданной области определения, и по ним построить график.

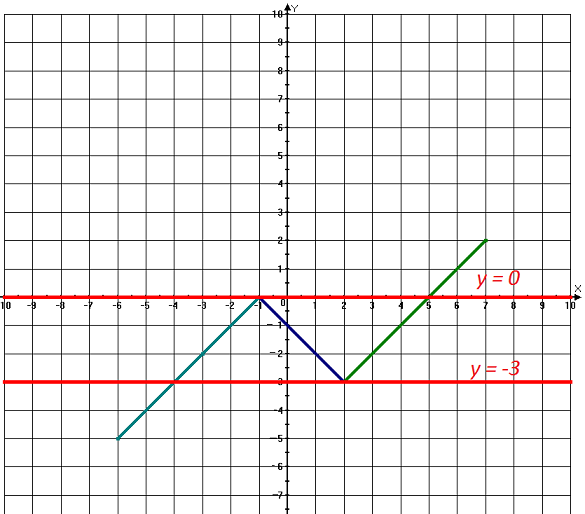
Прямая y = m имеет с графиком ровно две общие точки, если m = 0, m = -3.

Смотрите видеоурок с подробным решением задачи.

Если вам понравился материал, не поленитесь нажать на кнопочки любимой социальной сети и поделиться с друзьями.