Центральный и вписанный углы

Центральный и вписанный углы

Смотрите видеоурок:

*Если на окружности отметить две точки, они разделят окружность на две дуги.

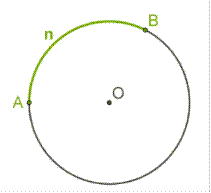 У каждой дуги есть градусная мера. Сумма градусных мер двух дуг с общими концами равна 360°.

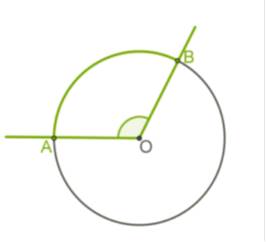
*Угол с вершиной в центре окружности называется центральным углом.

*Градусная мера центрального угла равна градусной мере соответствующей дуги окружности:

*∡ AOB= ∪AB.

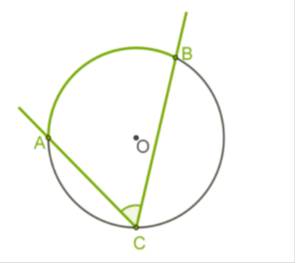
*Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

*Вписанный угол измеряется половиной дуги, на которую он опирается:

*∡ACB=0,5∪AB.

* Если отрезок, соединяющий концы дуги, является диаметром окружности, то дугу называют полуокружностью. Градусная мера полуокружности равна 180°.

*Вписанный угол, опирающийся на полуокружность, равен 90°.

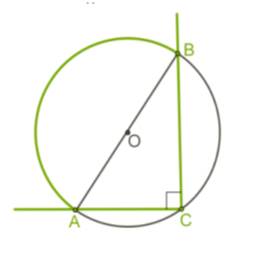
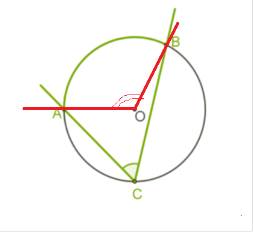
*Если центральный угол и вписанный опираются на одну и туже дугу, они называются соответственными.

*В этом случае градусная мера вписанного угла в 2 раза меньше градусной меры центрального угла.

*∠АСВ=1/2∠АОВ