Окружность, касательная, секущая, хорда
В плоскости прямая и окружность могут пересекаться или не пересекаться. При пересечении могут иметь одну или две общие точки.
Смотрите видеоурок:
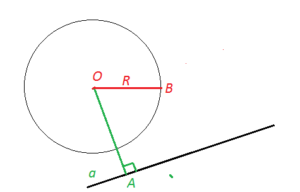
Если расстояние от центра окружности до прямой больше радиуса, то у прямой и окружности общих точек нет.
OA>R
Если расстояние от центра окружности до прямой равно радиусу, то у прямой и окружности одна общая точка.
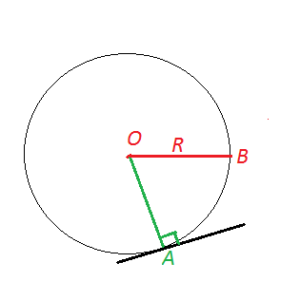
OA=R
Тогда прямая называется касательной к окружности.
Касательная перпендикулярна радиусу, проведенному к точке касания.
Если расстояние от центра окружности до прямой меньше радиуса, то у прямой и окружности две общие точки.
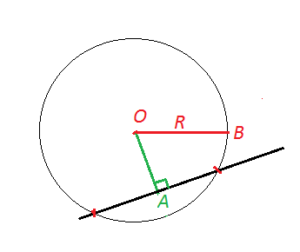
OA<R
Тогда прямая называется секущей к окружности.
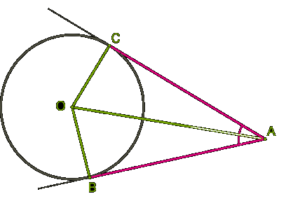
Если из точки к окружности проведены две касательные, то
а) длины отрезков касательных от этой точки до точки касания равны:
АВ = АС
б) прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам.
АО – биссектриса угла А
в) треугольники равны:
△ВОА=△СОА
Отрезок, соединяющий две точки окружности, называется хордой.
Диаметр (радиус), перпендикулярный хорде, делит ее пополам.
Так же пополам делится дуга, которую стягивает эта хорда.
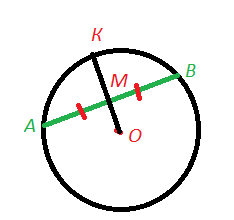
Если ОК⊥АВ,то АМ=ВМ
Дуга АК равна дуге ВК
Дуги, заключенные между параллельными одинаковыми хордами, равны.
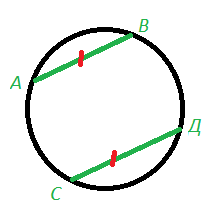
Если АВ∥СД и АВ = СД ,
то дуга АВ равна дуге СД.




















![]:-> ]:->](https://ogematematika.ru/wp-content/themes/ab-inspiration/inc/qipsmiles/smiles/devil.gif)























