Трапеция вписанная в окружность и ее свойства

Какими свойствами обладает трапеция, вписанная в окружность? 

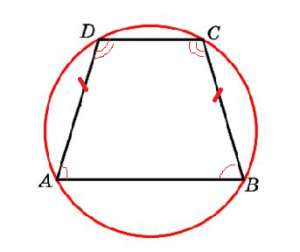
Трапеция — это четырехугольник. А четырехугольник можно вписать в окружность только тогда, когда сумма противолежащих углов составляет 180 градусов.
А это возможно только в равнобокой трапеции. То есть, только равнобокую трапецию можно вписать в окружность.

Давайте вспомним свойства равнобокой трапеции.

• В равнобокой трапеции угла при основаниях равны.
  

  ∠А = ∠С,  ∠В = ∠D

• В равнобокой трапеции (как и в любой трапеции) сумма углов, прилежащих к боковой стороне, составляет 180 градусов.
  

  ∠А + ∠D = 180,  ∠B + ∠С = 180

• В равнобокой трапеции сумма противолежащих углов составляет 180 градусов.
  

  ∠А + ∠С= 180,  ∠B + ∠D = 180

• В равнобокой трапеции диагонали равны.
  
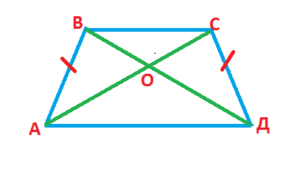
  АС = ВD
• Верхний и нижний треугольники подобны.
  ΔАОD ∼ ΔCOB
• Левый и правый треугольники равны.
  ΔАОВ = ΔCOD
• Если в равнобокой трапеции провести высоты от одного основания к другому, то на большем основании они отсекут равные отрезки (и равные прямоугольные треугольники).
  
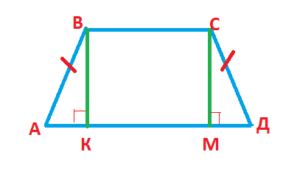
  АК = ДМ,      ΔАКВ = ΔДМС

Свойства трапеции равнобокой и трапеции, вписанной в окружность, часто можно встретить при решении задач. Поэтому нужно их помнить.

Хотите иметь справочные материалы со свойствами основных геометрических фигур всегда под рукой?

Тогда скачайте справочник в видеоформате.

«Видеошпаргалки по геометрии»