При каком значении p прямая y=-2x+p имеет с параболой y=x^2+2x ровно одну общую точку

При каком значении p прямая y=-2x+p имеет с параболой y=x^2+2x ровно одну общую точку

При каком значении p прямая y=-2x+p имеет с параболой y=x^2+2x ровно одну общую точку? Найдите координаты этой точки., Постройте в одной системе координат данную параболу,и прямую при найденном значении p.

• ОДЗ данных функций – вся числовая прямая.

Найдем значение параметра р.
Так как прямая  и парабола  пересекаются в одной точке, то координаты этой точки будут общими для обеих функций.

Тогда можно приравнять функции.

Получаем уравнение

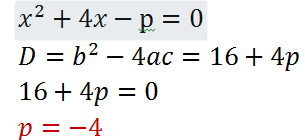
Так как общая точка у графиков одна, то уравнение должно иметь один корень. Следовательно, его дискриминант должен быть нулевым.

Вычислим координаты точки пересечения.
Для этого подставим найденное значение параметра в уравнение

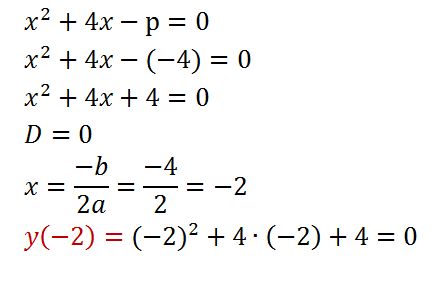
Итак, координаты точки пересечения графиков: (-2; 0)

Далее будем строить графики функций.

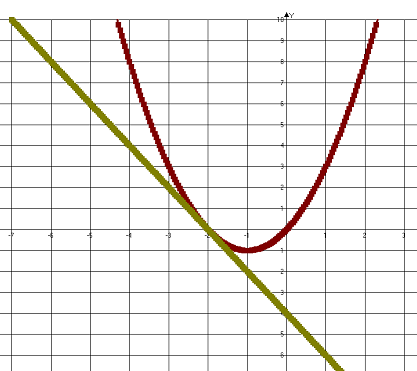
Ответ: р = -4; (-2; 0)

Смотрите видеоурок с подробным решением данной задачи.