Прямая имеет с графиком ровно одну общую точку

Постройте график функции  и определите, при каких значениях параметра  прямая  имеет с графиком ровно одну общую точку.

Задача имеет довольно длинное решение, которое делится на несколько этапов.

1. Найдем ОДЗ. Функция представляет собой дробное выражение, поэтому из области допустимых значение переменной выпадают те числа, которые обращают знаменатель дроби в ноль. Это числа 3 и — 2.
2. Разложим на множители числитель дроби (для этого нужно решить биквадратное уравнение), затем сократим ее.
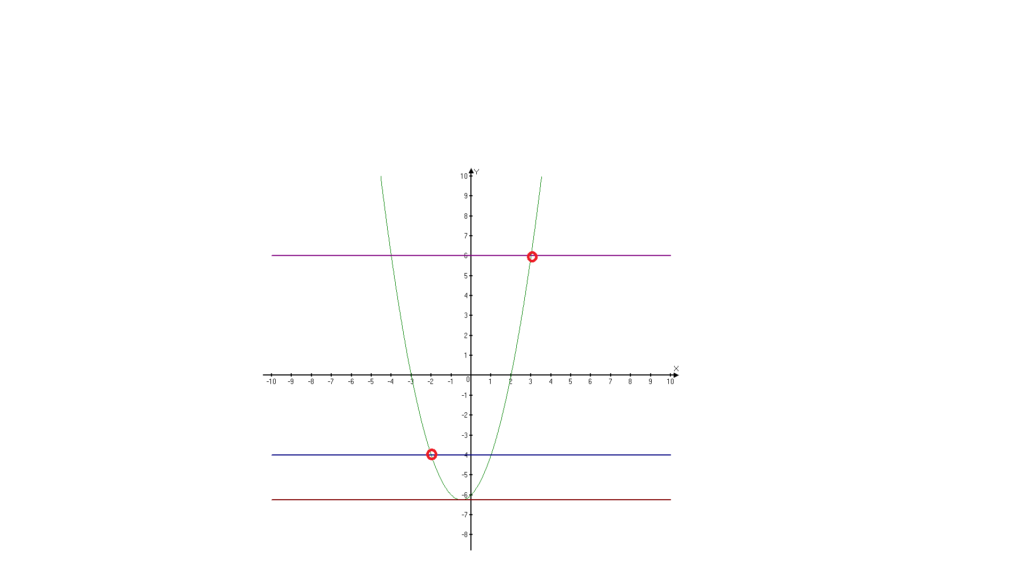
3. Получилась квадратичная функция. Вычислим координаты нескольких точек (координаты вершины параболы, нули функции, точку пересечения параболы с осью ординат и координаты «выколотых» точек.)
4. По этим точкам проведем параболу.
5. Определим значения параметра с, при котором прямая y = c пересекает параболу ровно в одной точке. Таких значений здесь будет три.

   Получается вот такой чертеж:
   Смотрите видеоурок с подробным решением данной задачи.