при каких значениях m прямая y = m не имеет с графиком ни одной общей точки

Постройте график функции   и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.

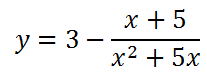
Так как функция содержит дробное выражение, то нужно найти область допустимых значений переменной.

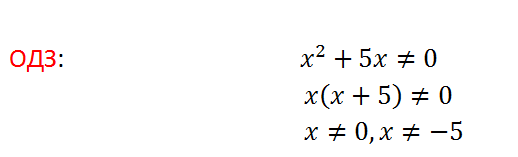
Упростим функцию.
Для этого разложим на множители знаменатель, затем сократим дробь.

Далее заполним таблицу значений функции, чтобы хотя бы по нескольким точкам изобразить гиперболу.

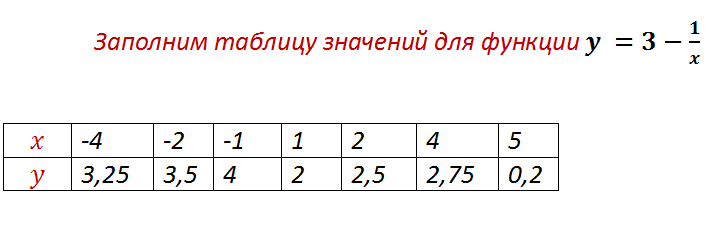
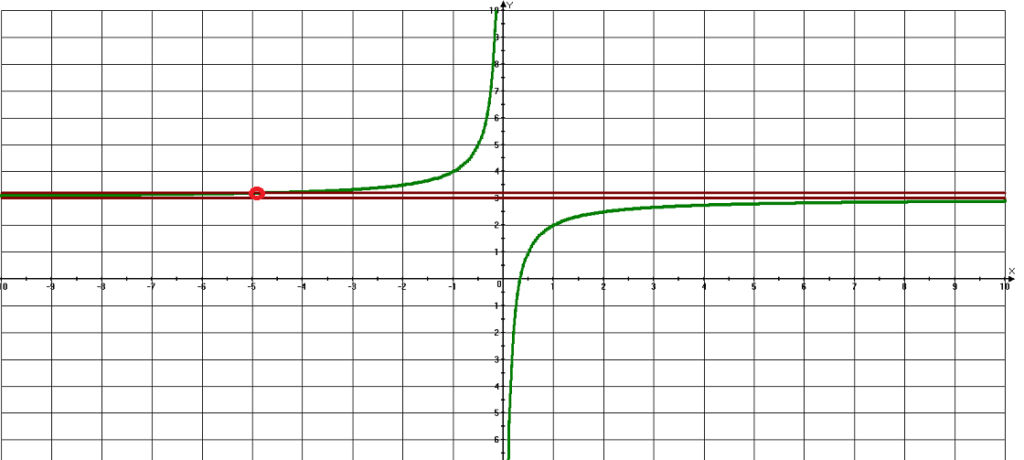
Графиком данной функции является гипербола, которая получается из гиперболы y=-1/x путем сдвига на 3 единицы вверх.

То есть, прямая y=3 будет служить горизонтальной асимптотой для гиперболы.

(Асимптота – это прямая, к которой неограниченно близко приближается график функции, но не пересекает ее)

Найдем координаты выколотой точки.

Выколотая точка имеет координаты (- 5; 3,2)

Прямая  не будет иметь с гиперболой  общих точек в двух случаях: если она  будет проходить через выколотую точку (y=3,2)   и через горизонтальную асимптоту (у=3) .

Построим график функции.

Смотрит видеоролик с подробным решением задачи.