Окружность и четырехугольник

Окружность и четырехугольник

*Если все стороны четырёхугольника касаются окружности, то он называется четырёхугольником, описанным около этой окружности, а окружность — вписанной в четырёхугольник.

Смотрите видеоурок:

*В четырехугольник можно вписать окружность, если суммы противоположных сторон четырёхугольника равны.

AB +CD = AD + DC

Окружность можно вписать в квадрат, ромб, произвольную трапецию, прямоугольную трапецию, равнобедренную трапецию.

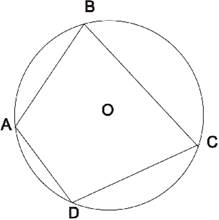
*Четырёхугольник, все вершины которого лежат на окружности, называется вписанным в эту окружность, а окружность называется описанной около четырёхугольника.

*Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.

*         ∠А+∠С=∠B+∠D=180

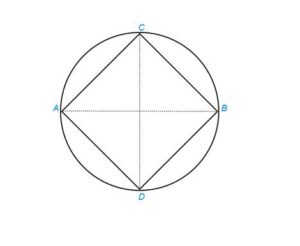
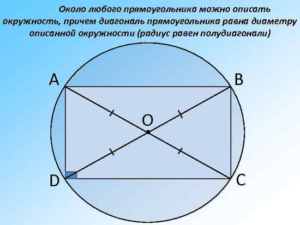
Окружность можно описать вокруг любого квадрата, прямоугольника, равнобокой трапеции.

Центр окружности лежит в точке пересечения диагоналей.

Около произвольного параллелограмма или ромба нельзя описать окружность.

*Радиус описанной окружности квадрата равен половине его диагонали

*          R=d/2

*Если выразить радиус через сторону квадрата, то получим формулу

*                R=(a√2)/2

Радиус описанной окружности прямоугольника тоже равен половине его диагонали

*      R=d/2

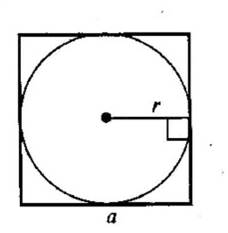
*Радиус вписанной окружности квадрата равен половине его стороны.

*       r=a/2

Радиус окружности, вписанной в трапецию, равен половине ее высоты.

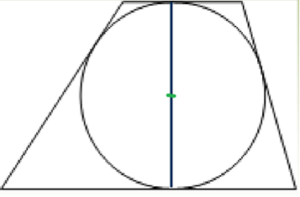
*       r=h/2