Окружность и треугольник
*Окружность называют описанной около треугольника, если все вершины треугольника расположены на окружности.
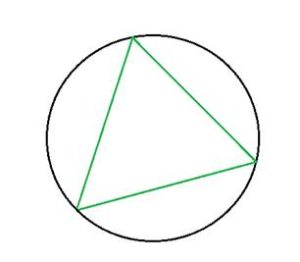
Смотрите видеоурок:
*Её центр равноудалён от всех вершин, то есть должен находиться в точке пересечения серединных перпендикуляров к сторонам треугольника.
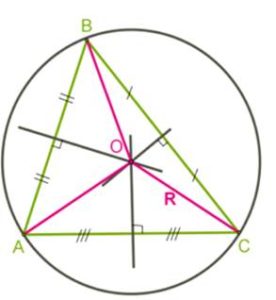
*Следовательно, около любого треугольника можно описать окружность, так как серединные перпендикуляры к сторонам пересекаются в одной точке.
*Для остроугольного треугольника центр окружности находится в треугольнике.
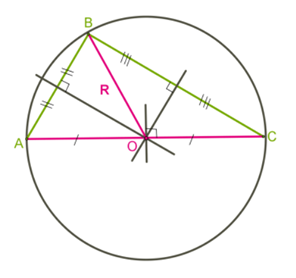
*Для прямоугольного треугольника центр окружности находится на середине гипотенузы.
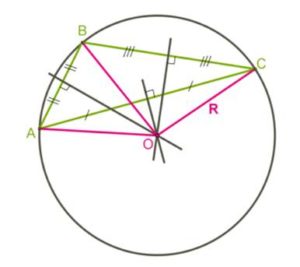
*Для тупоугольного треугольника центр окружности находится вне треугольника.
*Окружность называют вписанной в треугольник, если все стороны треугольника касаются окружности.
*Её центр равноудалён от всех сторон, то есть должен находиться в точке пересечения биссектрис треугольника.
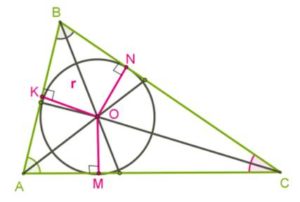
Следовательно, в любой треугольник можно вписать окружность, так как биссектрисы треугольника пересекаются в одной точке.
Так как биссектрисы углов треугольника всегда пересекаются внутри треугольника, то для всех треугольников центр вписанной окружности находится в треугольниках.
*У равностороннего треугольника совпадают биссектрисы, медианы и высоты, то есть, эти отрезки являются также серединными перпендикулярами.
*Это значит, что центры описанной и вписанной окружности совпадают.
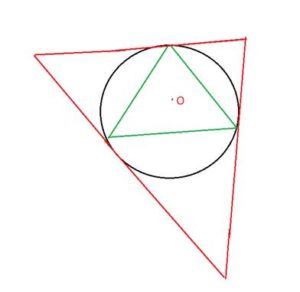
*Радиус окружности, описанной около равностороннего треугольника.
R=2/3 h, R=(a√3)/3.
*Радиус окружности, вписанной в равносторонний треугольник.
r=1/3 h, r=(a√3)/3.




















![]:-> ]:->](https://ogematematika.ru/wp-content/themes/ab-inspiration/inc/qipsmiles/smiles/devil.gif)























