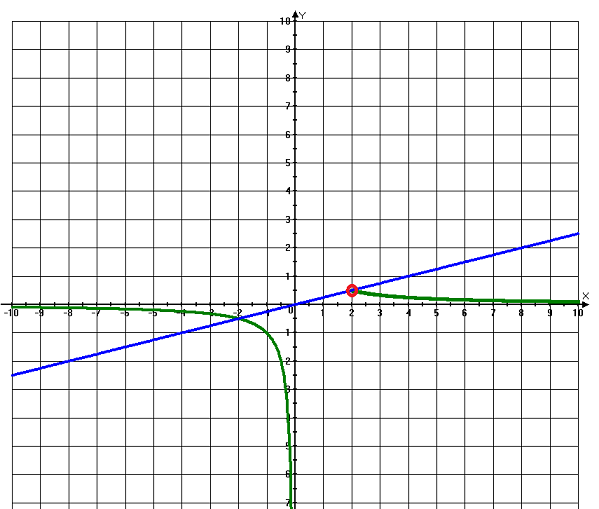
Постройте график функции и найдите все значение , при которых прямая имеет с графиком данной функции ровно одну общую точку.

Найдем ОДЗ, исходя из двух соображений:
Арифметический квадратный корень имеет смысл только из неотрицательных чисел.
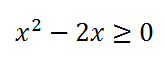
Но данное выражение находится в знаменателе дроби, следовательно, нулю оно равняться не может. Поэтому неравенство должно быть строгим.
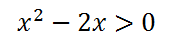
Решим его методом интервалов.
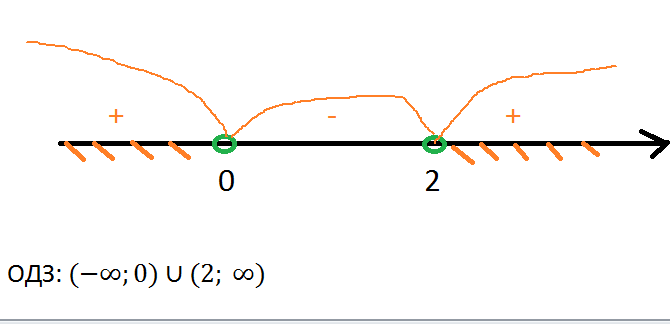
Теперь упростим выражение.
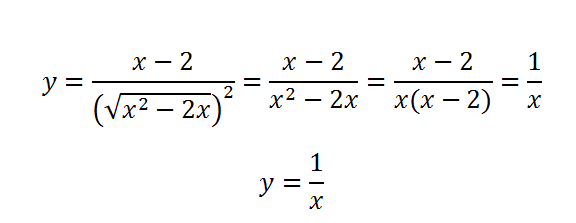
Выколотая точка, в которой происходит разрыв гиперболы, имеет координаты
(2; 0,5).
Подставив эти координаты в уравнение прямой y = kx, найдем граничное значение параметра k.
k = 0,25
Таким образом, прямая y = kx пересекает график в одной точке при все значениях k, больше или равно, чем 0,25.
Ответ:
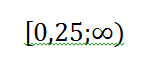




















![]:-> ]:->](https://ogematematika.ru/wp-content/themes/ab-inspiration/inc/qipsmiles/smiles/devil.gif)























