Кусочно-непрерывные функции. Урок 1

Кусочно-непрерывные функции. Урок 1

Постройте график функции   и определите, при каких значениях параметра  с прямая y=c  имеет с графиком ровно одну общую точку.

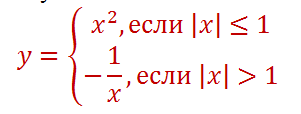
Разделим функцию на две части, и с каждой частью будем работать отдельно.

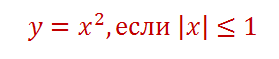
Областью определения функции является промежуток

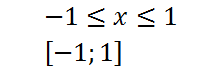
График функции  на этом промежутке будет парабола с вершиной в начале координат. Ветви направлены вверх.

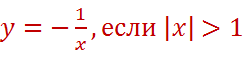
Областью определения функции является объединение промежутков:

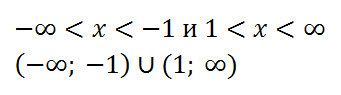
Причем точка с абсциссой 1 будет выколотой.

Графиком данной функции  служит гипербола, лежащая во II  и IV четвертях с горизонтальной асимптотой y=0 (осью абсцисс).

(Асимптота – это линия, к которой график функции неограниченно приближается, но не пересекает ее).

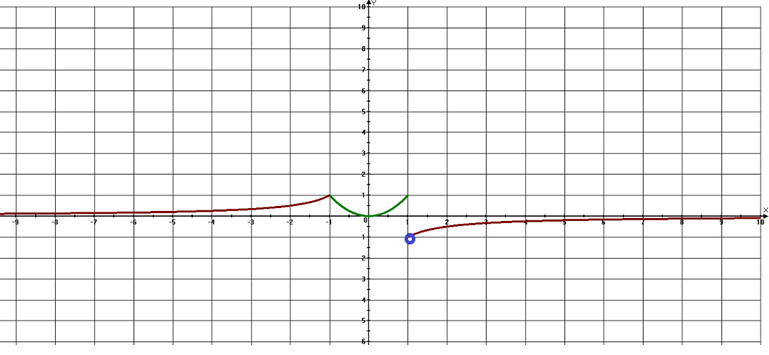
Прямая   y=c будет иметь с графиком одну общую точку на промежутке (-1; о]

Ответ: (-1; о]

Смотрите видеоурок с подробным решением задачи.