Кусочно-непрерывная функция. Урок 4

Постройте график функции и найдите все значения , при которых прямая не имеет с графиком данной функции общих точек.

Найдем ОДЗ, исходя из двух соображений:
1)Арифметический квадратный корень имеет смысл только из неотрицательных чисел. (Подкоренное выражение должно быть больше или равно нулю).
2) На ноль делить нельзя (Из ОДЗ выпадает число 3).

Составим неравенство и решим его методом интервалов.

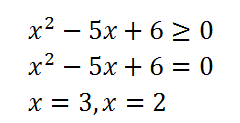
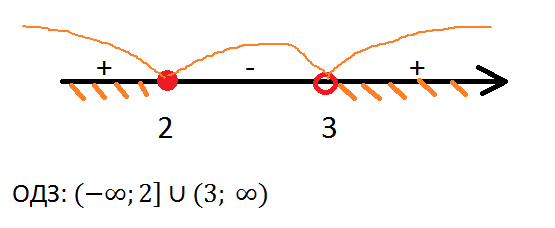
Теперь упростим выражение, которое содержит функция.

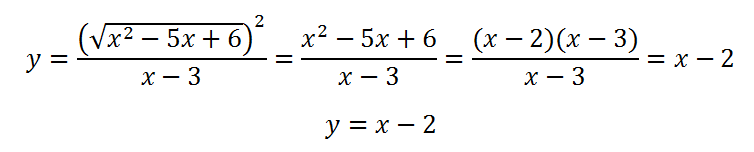
Это линейна функция. Графиком функции служит прямая, только она будет иметь разрыв.

Разрыв графика на промежутке (2; 3]

Функция на этом промежутке принимает значения (0; 1]

Таким образом, прямая y = a не имеет с графиком общих точек при значении a от 0 до 1.

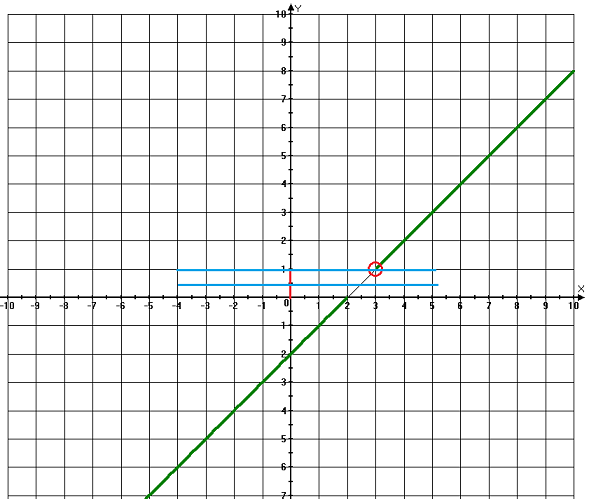
Ответ: (0; 1]

Смотрите видеоурок с подробным решением задачи.