Постройте график функции и определите, при каких значениях k прямая y = kx не имеет с графиком общих точек.

Вспомним модуль числа.
|x| = x, если x
|x| = — x, если x < 0
Преобразуем функцию.

Найдем несколько основных точек для каждой гиперболы и схематично их изобразим.
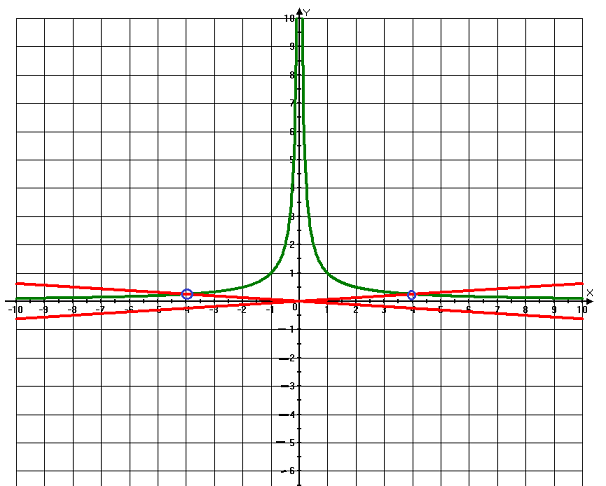
Прямая y = kx не имеет с графиком общих точек в трех случаях;
1)Она проходит через выколотую точку (4; 0,25),
2)Она проходит через выколотую точку (-4; 0,25),
3) Либо k=0. Тогда y = 0 (прямая проходит по оси абсцисс).
Зная координаты выколотых точек, можно найти значение k.
Зная координаты выколотых точек, можно найти значение k.
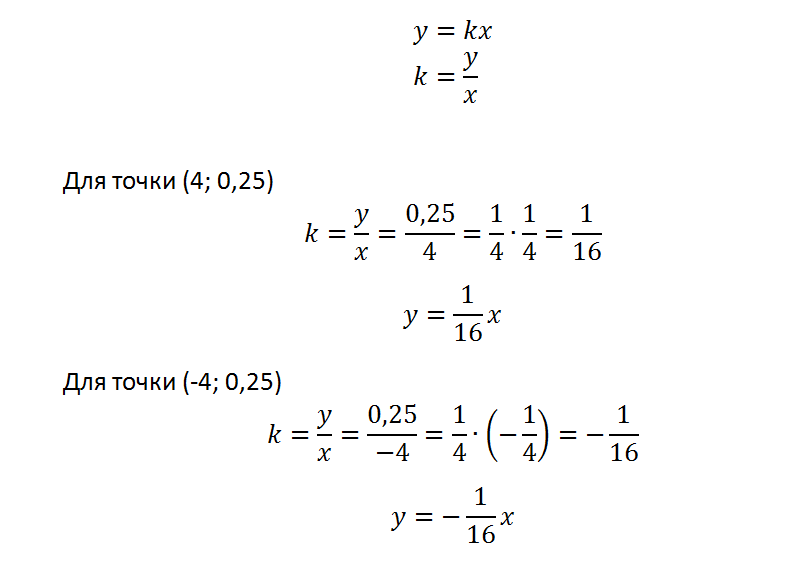
Ответ: 0; 1\16; -1\16.
Смотрите видеоурок с подробным решением задачи.
Если вам понравился материал, не поленитесь нажать на кнопочки любимой социальной сети и поделиться с друзьями.




















![]:-> ]:->](https://ogematematika.ru/wp-content/themes/ab-inspiration/inc/qipsmiles/smiles/devil.gif)























