Свойства числовых неравенств

Выражение, содержащее знаки > , <, называется неравенством.

Смотрите видеоурок:

Свойство 1. Если a > b и b >c, то a >c.

Свойство 2. Если a > b, то a + c > b + c.

Если к обеим частям неравенства прибавить одно и то же число, то знак неравенства не изменится.

Свойство 3. Если a > b и k > 0, то ak > bk.

Если обе части неравенства умножить (или разделить) на одно и то же положительное число, то знак неравенства не изменится.

Свойство 4. Если a > b и k < 0, то ak < bk.

Если обе части неравенства умножить (или разделить) на одно и то же отрицательное число, то знак неравенства изменится (< на >, > на <).

Свойство 5. Если a > b, то 1/a <1/b

А также нужно помнить, что слагаемое можно переносить из одной части неравенства в другую, поменяв его знак на противоположный.

Системы линейных неравенств с одной переменной решаются достаточно просто.

Каждое неравенство решается отдельно, а потом записывается общее решение.

Решение неравенства часто изображается на координатной прямой. И здесь нужно помнить некоторые особенности изображения и записи числовых промежутков.

Чем число больше, тем оно правее; чем число меньше, тем оно левее.
Если неравенство строгое, то точка на координатной прямой «выколотая» (прозрачная). Скобка круглая.
x > 2.
Если неравенство нестрогое, то точка на координатной прямой заштрихованная. Скобка квадратная.
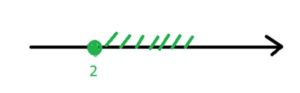
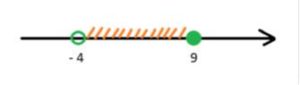
Двойное неравенство ограничено с двух сторон