Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг

Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?

Сделаем рисунки, потому что сразу станет понятней.

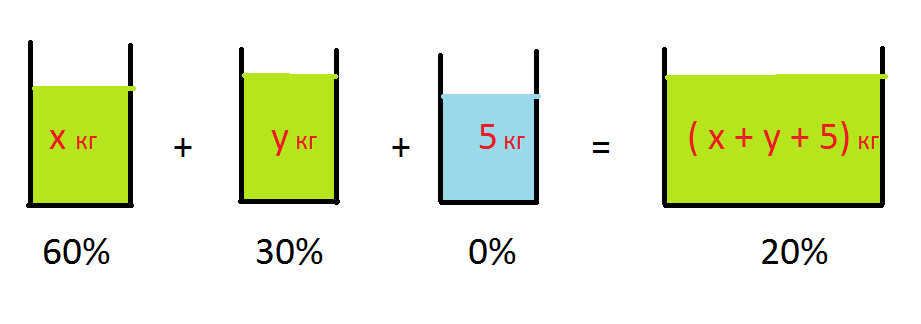
Пусть x кг — масса первого раствора, y кг — масса второго раствора.

Тогда (x + y +5) кг — масса получившегося раствора.

Составим уравнение относительно масс кислоты.

Используем первое условие: Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты.

Так как концентрация первого раствора 60%, то кислоты в нем содержится 0,6 x кг. Масса кислоты во втором растворе 0, 3 x кг.
Масса кислоты в новом растворе 0,2 (x + y + 5) кг.

Получаем:

0,6 x кг + 0, 3 x кг + 0*5 = 0,2 (x + y + 5)

Теперь рассмотрим второе условие: Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты

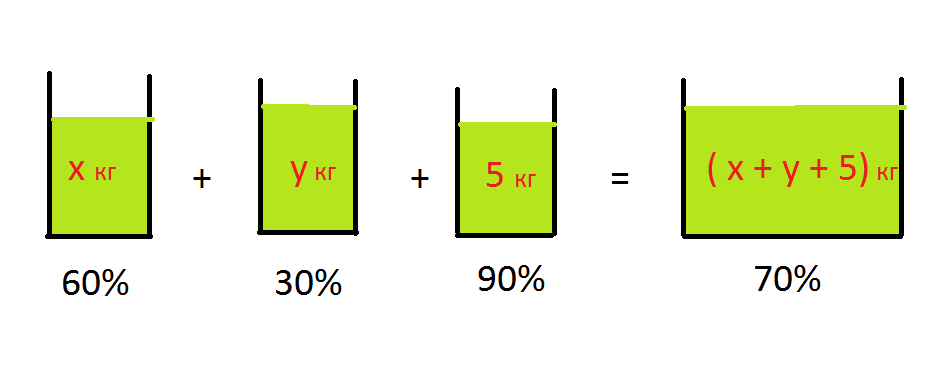0,6 x кг + 0, 3 x кг + 0,9*5 = 0,7 (x + y + 5)