Прямая и гипербола имеют одну общую точку

Постройте график функции  и определите, при каких значениях  k прямая  y = kx  имеет с графиком ровно одну общую точку.

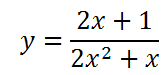
Так как функция содержит дробное выражение, обязательно нужно найти область допустимых значений переменной.

ОДЗ:

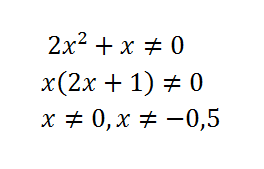
Упростим функцию.
Для этого разложим на множители знаменатель, затем сократим дробь.

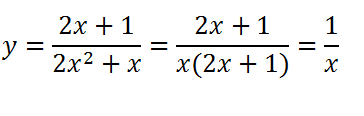
Функция приобрела вид y = 1/x.

Это функция обратной пропорциональности. Ее графиком является гипербола, состоящая из двух ветвей.

Заполним таблицу значений, чтобы по точка построить график функции.

Прямая y = kx будет иметь с гиперболой y = 1/x одну общую точку только в том случае, если она пройдет через выколотую точку (-0,5; -2).

Подставив координаты этой точки в формулу функции y = kx, определим значение параметра k.

k = 4

Теперь осталось построить графики функций и записать ответ.

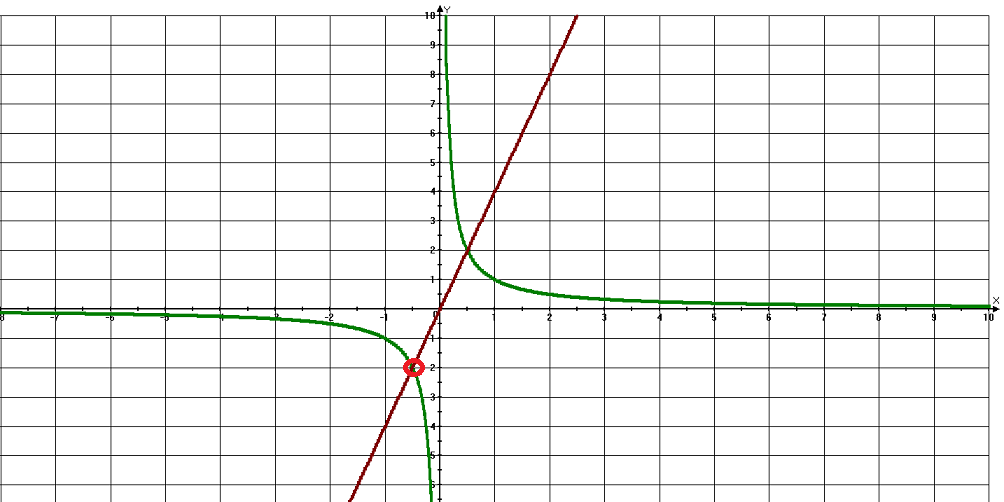
Ответ: 4

Смотрите видеоурок с подробным решением задачи.

В комментариях пишите, какие темы вызывают у вас затруднения.

Если вам понравился материал, не поленитесь — нажмите на кнопочки любимой социальной сети, чтобы поделиться с друзьями.