Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации

Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации.

Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 33% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом растворе?

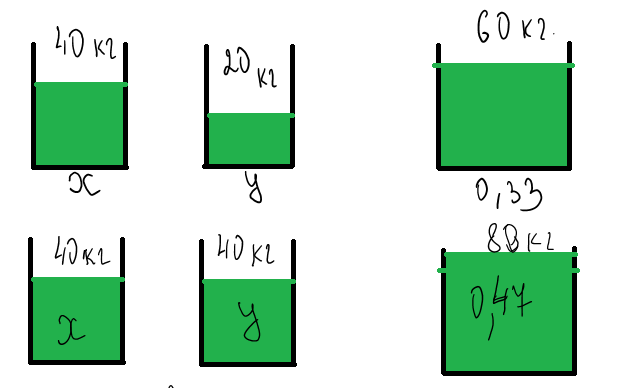
Обозначим за x концентрацию кислоты в первом сосуде, а за y — концентрацию кислоты во втором сосуде.

Тогда масса кислоты в первом сосуде будет 40x, а во втором — 20y.

Отсюда получаем первое уравнение

40x + 20y = 60*0,33

Теперь используем второе условие: если слить равные массы растворов. Допустим, возьмем по 40 кг каждого раствора.

Получаем второе уравнение

40x + 40y =  80*0,47

Чтобы вычисления были проще, первое уравнение сократим на 20, а второе на 40.

2x + y = 0,99
x + y  = 0,94

Видим, что данную систему проще решить способом сложения.

Умножим второе уравнение на -1, затем сложим и сразу найдем значение x.

А затем вычислим массу кислоты в первом сосуде, как 40x

Смотрите видеоурок, там все подробно.

И обязательно поставьте видео на паузу. Решите эту задачу на сами. Только тогда информация из видео принесет вам пользу.