Найдите угол АСО, если его сторона СА касается окружности

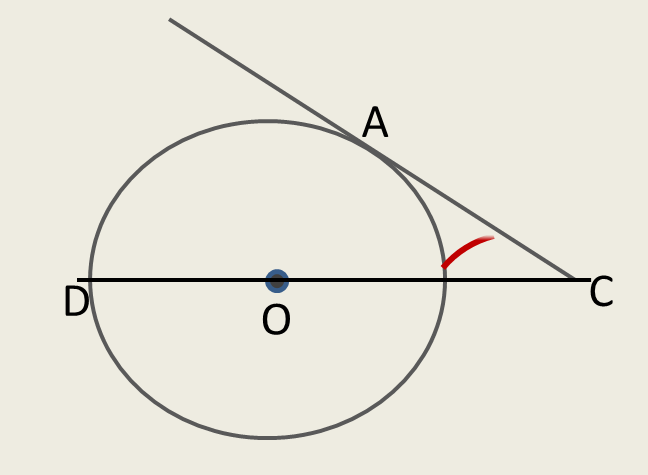
Найдите угол АСО, если его сторона СА касается окружности

Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 100°.

Проведем радиус ОА. Получаем центральный угол ДОА, величина которого равна градусной мере дуги АД, на которую этот угол опирается, то есть угол ДОА = 100 градусов.

Угол СОА — смежный с углом ДОА, и тогда его градусная мера равна 80 градусам (смежные углы в сумме составляют 180 градусов).

Так как ОА — радиус, проведенный в точу касания, то он перпендикулярен касательной.

Тогда угол ОАС прямой.

Треугольник ОАС — прямоугольный. Следовательно, сумма острых углов равна 90 градусов.

СОА + АСО = 90.

Тогда искомый угол АСО = 90 — 80 = 10 градусов.

Ответ: 10

Смотрите видеоурок с подробным решением задачи.