Геометрический смысл производной заключается в следующем утверждении:
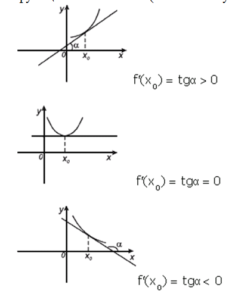
Если функция дифференцируема в точке , то производная функции в этой точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке (или тангенсу угла наклона).
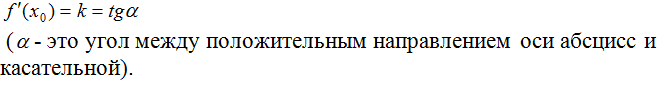
Если угол острый, то тангенс угла наклона (и, соответственно, значение производной в точке, и угловой коэффициент) положителен.
Если угол тупой, то тангенс угла наклона (и, соответственно, значение производной в точке, и угловой коэффициент) отрицателен.
Если угол равен нулю (касательная в этом случае расположена горизонтально, то есть, параллельна оси абсцисс), тангенс угла наклона и угловой коэффициент прямой тоже нулевые.
Угловой коэффициент касательной можно вычислить по формуле Лагранжа:
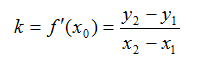
Этой формулой удобно пользоваться, если на касательной даны две точки с известными координатами, либо можно самим взять какие-либо две удобные точки, координаты которых точно можно найти по графику.
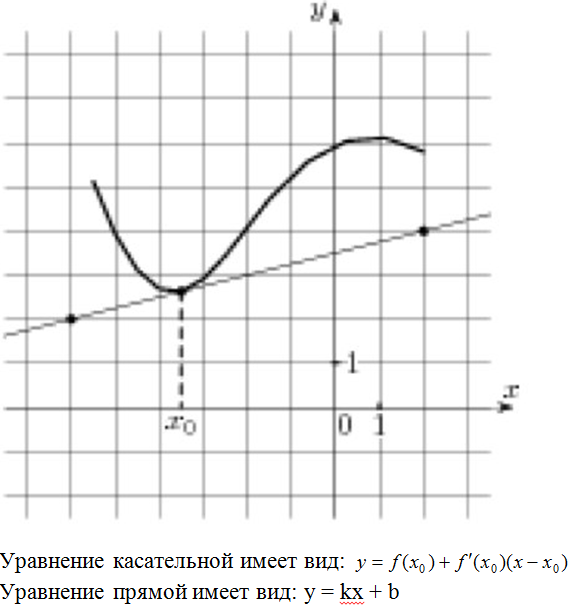




















![]:-> ]:->](https://ogematematika.ru/wp-content/themes/ab-inspiration/inc/qipsmiles/smiles/devil.gif)























